

For now, we’ll focus on the purpose and the mechanics of data visualizations. These include the scatter plot, histogram, boxplot, and bar graph. In this session, we’ll learn a few useful graphic functions. Well-designed data visualizations present your data to your audience in a way that is easy to comprehend.īuilding graphics in R is relatively simple. Visualizations are helpful both to you as a data analyst and your audience.
#Two box plots same graph r how to
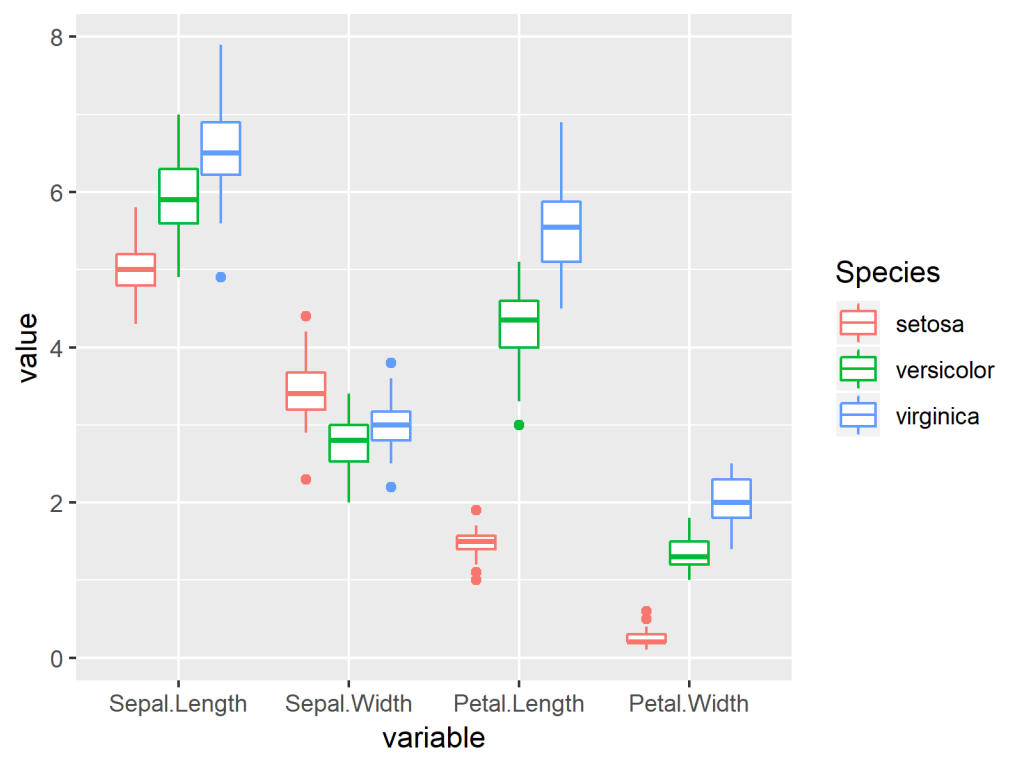
In this session, we are going to learn how to create several types of statistical visualizations. In session 4, we saw an example of a scatter plot and density plot. 8 Interactive Applications Using RShiny.Limitations of box plots, and better alternatives.Box plots skewed to the right? To the left?.Ranges vs counts: a common mistake while reading box plots.How to compare box plots with overlapping medians.If you want to know what else is in the box (hah, see what I did there?), check out this post.
#Two box plots same graph r software
Finally, look for outliers if there are any.īioVinci is a drag-and-drop software that will let you make a box plot in just a few minutes. Then check the sizes of the boxes and whiskers to have a sense of ranges and variability. First, look at the boxes and median lines to see if they overlap. That’s a quick and easy way to compare two box-and-whisker plots. Data points have to go above or below the box pretty far to count as outliers. When there are outliers, they are dotted outside the whiskers. Wider ranges (whisker length, box size) indicate more variable data. That’s something to look for when comparing box plots, especially when the medians are similar.
Short boxes mean their data points consistently hover around the center values. The same thing can be said about the boxes. Larger ranges indicate wider distribution, that is, more scattered data. Together with the box, the whiskers show how big a range there is between those two extremes. The lines coming out from each box extend from the maximum to the minimum values of each set. If both median lines lie within the overlap between two boxes, we will have to take another step to reach a conclusion about their groups. If the median line of box A lies outside of box B entirely, then there is likely to be a difference between the two groups.īoxes overlap but don’t spread past both medians: groups are likely to be different. These are the medians, the “middle” values of each group. If they overlap, move on to the lines inside the boxes. Non-overlapping boxes, groups are different. If two boxes do not overlap with one another, say, box A is completely above or below box B, then there is a difference between the two groups. They represent the interquartile range, or the middle half of the values in each group. The key information you want to get when reading box plots is: are these groups different, and if so, how? To quickly compare box plots, look for these things: The boxes: But box plots are not always intuitive to read.

They manage to carry a lot of statistical details - medians, ranges, outliers - without looking intimidating. box-and-whiskers plots, are an excellent way to visualize differences among groups.


 0 kommentar(er)
0 kommentar(er)
